Distributed Hash Table in the Era of Internet of the Things

Kademlia's Bucket Dilemma When the Address Space Size is Large ( for instance 512 ).
Click on this link for the companion site

Aim:

New projects are designing a peer to peer network for Internet of the things with a structured perspective, to be reasonably /& sufficiently adaptive and secure by exploiting all potentiality in cryptography hashes and distributed hash tables. The distributed hash tables (DHTs) are required:

To enable nodes forming a structured overlay network ( fully decentralized).
To be secure against faulty participants.
To be reliable against churn ( nodes continuously joining, leaving, and failing).
To be scalable and should function efficiently even with thousands, millions or billions of peers.

The DHTs are not only used to distribute and retrieve a content between the peers but also if possible to enable secure consensus to send automatically messages between peer endpoints and meshing a secure peer to peer network between all endpoints for a specific business purpose.

The Kademlia DHT uses an algorithm to define the closest peer IDs to a given peer ID accordingly to XOR distance.

Kademlia routing tables based on the concept of buckets over XOR space. The nodes IDs sharing a number of bits with a target ID are stored in the associated bucket. When the address space size is large, this concept of bucket begins to be very blurred. For instance when the address space size is 512, half of the peer IDs will be in bucket 511, bucket 510 will have 1/4, bucket 509 will have 1/8 and so on.

So the probability to have a peer ID in bucket "M"is 2^(M-512), when M is small, this probability is quasi-zero. Many buckets are just empty. Taking the traditional set-up for each k-bucket having k=20 peers only, the Kademlia's DHT will provide a routing table less than the maximum number 511*20 ~ 10220 peers for each given peer. Numerical simulation showed using 50000 peers that only the first 10 buckets are slightly filled by around or less than 200 peer IDs.

This Bin representation for measuring the closest peer IDs to a given peer ID is blunt when the address space size is large. We need a clear-eyed process regarding the real spatial distribution of values than lumping the values into a Logbins framework.

We need to investigate new representation of XOR distance to successfully be used in the arising applications of HDTs, especially in Internet of the things.

This work focuses on quality measures of XOR distance when address space size is large, for instance 512.

We measure the quality by using the concept of the discrepancy. We perform computational investigations to compare the performance of the random numbers with that of the sets of XOR distances. The investigation enables us to better understand the distributional properties of XOR values and throws new light on when and why using directly the values from XOR distance can have a better (or no better) performance than bin Kademlia concept( Buckets).

We provide a numerical analysis of Kademlia when the address space size is 512 ( many recent interesting projects related to the Internet of the things are based on keys in the XOR space having an address space size 512).

Main Operation is FindNode: Find K closest peer IDs to a given peer ID (Key)

Given a peer ID (A0) and a number of peer IDs ( A1,A2,A3, ... An) , we study the propriety of the sequence XOR(A0,Ai) when (1<= i <=N) and XOR(A0,Ai) are considered a sequence of numerical values, big Endian numbers.

How well are their values distributed?

Statistically, when the IDs are randomly selected, the sequence XOR(A0,Ai) , 1<= i <= N follows an uniformly distribution.

Dispersion and Discrepancy in XOR Sequence:

We are interested by the following problem:

Is XOR sequence a low-discrepancy sequence?

Note that ordinary uniform random numbers and low discrepancy sequences both generate uniformly distributed sequences.

A uniform random source will generate outcome that each run has the same probability on equal sub-intervals. In general uniform random source may experience clumped or uncorrelated outcomes. A low discrepancy sequence are subject to low-discrepancy requirement.

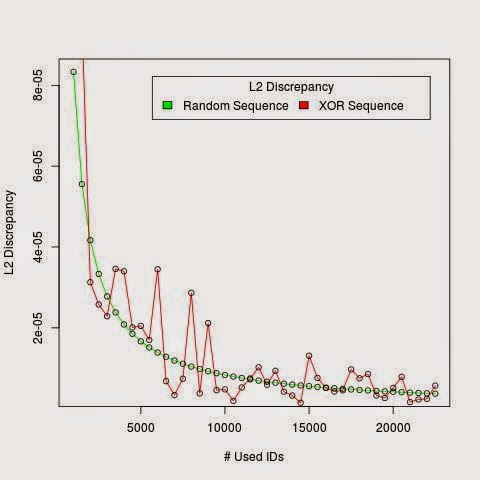
The L2 discrepancy value captures the global degree of isolation of the sequence of numbers in the given domain ( for instance (0,1)) which means that the higher the value of the L2 discrepancy is, the scarcer the numbers become in some parts of the domain.

For instance, if the values obtained from the XOR distance are tightly coupled, they will tend to occupy a small region of space and as a consequence, L2 discrepancy will be a higher value.

However, if the values obtained from the XOR distance are loosely coupled then, they are scattered over a large region of the domain. Thus, the L2 discrepancy will be a small value.

Figure below shows the results when a peer ID target was XORed by a number of peer IDs.

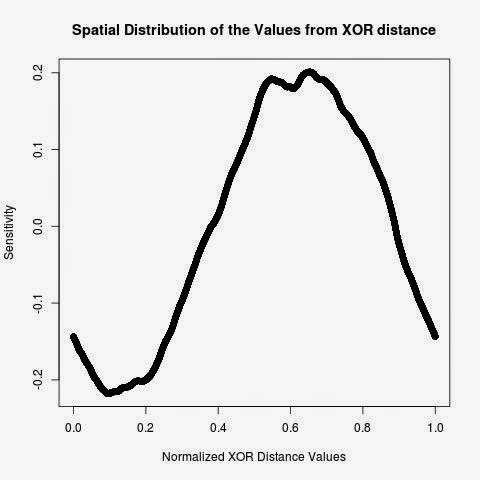
Each value from XOR distance will be represented by the value of the L2 Discrepancy sensitivity function, If the sensitivity is positive, the value from XOR distance is an insider otherwise it is an outlier. The sensitivity function is able to recover the spatial distribution of the values of XOR distance and their visibility, i.e. whether the values are uniform, clumped or scarce region, see Figure below.